Cleaning RV time series from stellar activity: SN-fit and bp-method
Dr. Andrea Bonfanti
Austrian Academy of Sciences, Graz
18 Novembre 2021 ore 11:00 – 12:00
Abstract
The radial velocity (RV) technique is one of the most successful method for detecting exoplanets and it is based on measuring the Doppler reflex motion induced on a star by its orbiting planets.
However, the stellar activity in the form of oscillations, granulations, spots or faculae also produces Doppler signals which may completely hide the Keplerian signal of an exoplanet.
Removing the stellar activity contribution from a RV time series is then crucial to hopefully detect an exoplanet.
While exoplanets produce a Doppler-shift on the CCF extracted from the stellar spectrum without modifying its shape or its width, active regions produce variations in both the asymmetry and the FWHM of the CCF.
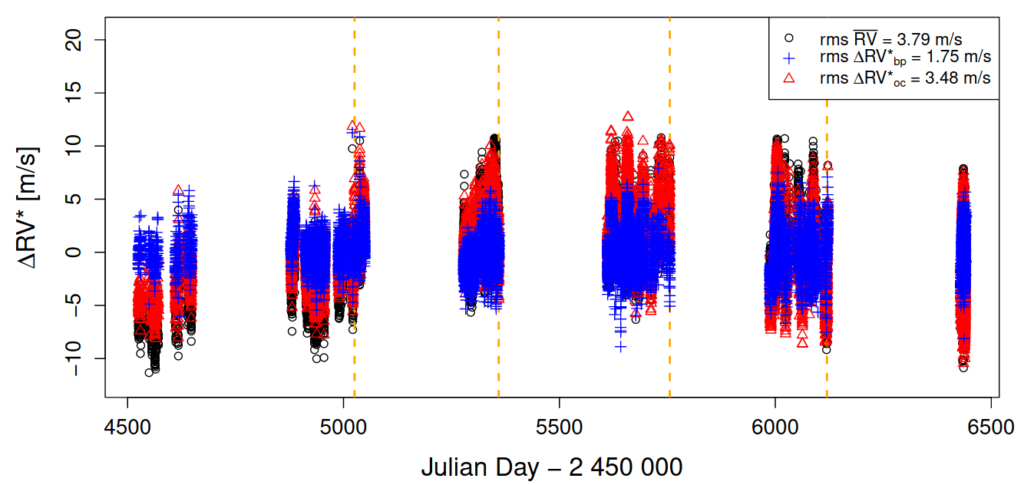
During my talk I will present a novel technique for removing stellar activity that can be divided in two steps. In the first step a Skew-Normal (SN) fit is applied to the CCF to retrieve not only the Doppler signal which constitutes the RV time series, but also the FWHM, the contrast, and the skewness of the fitted function. These hyperparameters are activity indicators, therefore they are employed during the second step, when the RV time series is cleaned from stellar activity.
To this end, I will present you the breakpoint (bp) method, which belongs to the family of change point detection algorithm.
In fact, if on the one hand the Keplerian signal is persistent along the RV time series, on the other hand active regions (hence their RVsignal) evolve over time.
The core idea of the bp method is to evaluate those locations along a time series where the correlation changes involving the activity indicators are statistically significant.
Applying a piecewise detrending rather than an overall correction (oc) turns out to be much more effective in removing the stellar activity contribution as shown by different examples where this framework has been applied.