The Gaia space mission obtains sparse photometric measurements for thousands of asteroids. At the end of mission, about 70 photometric measurements, obtained at different epochs, will be available for each object. These measurements will be exploited to determine for each asteroid the rotation period, the direction of its rotation axis, some properties of light scattering from its surface, and the overall shape. Photometric inversion is carried out using a numerical program adopting a “genetic” technique to determine the set of physical parameters of each object that best fit the available photometric data. As for shapes, for sake of simplicity two possible approximations are done: (1) the shape is assumed to be a triaxial ellipsoid; (2) the shape is assumed to be a so-called “cellinoid”, formed by the merging of eight octants of different triaxial ellipsoid, sharing the same values of their semi-axes in the regions were couple of octants are adjacent (see Figure). The name “cellinoid” is due to the fact that the first published scientific article making use of this shape for the study of asteroid photometry was authored by A. Cellino (Torino observatory) and collaborators, in 1990. The inversion program has been tested using the still preliminary catalogue of Gaia photometric data for asteroids, covering only about two years, published in the second Intermediate Data Release (DR2) of Gaia. The obtained results have been very encouraging. In spite of the fact that the available data cover a very short time span, it has been found that the preliminary inversions of a sample of DR2 data produce a correct determination of the spin period in most cases, for objects whose rotation periods have been determined using decades of ground-based photometric observations.
The paper entitled “Inversion of HIPPARCOS and Gaia photometric data for asteroids. Asteroid rotational properties from sparse photometric data” is available here:
https://ui.adsabs.harvard.edu/abs/2019A%26A…631A..67C/abstract
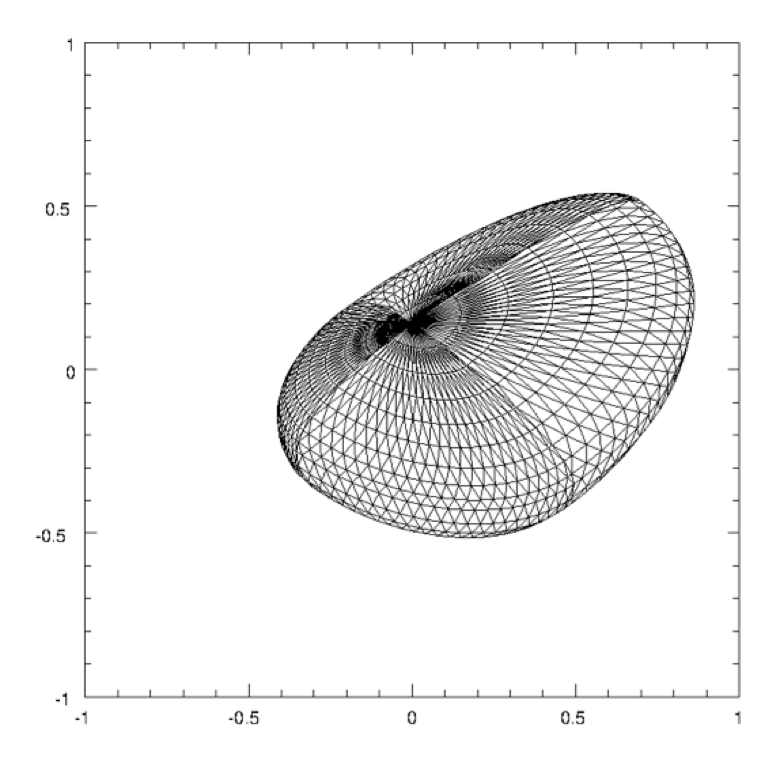
Example of a “cellinoid”. The object results from the merging of eight octants of triaxial ellipsoids. The semiaxes are equal to 1.0 and 0.5 in the resulting longest axis, 0.7 and 0.4 in the intermediate axis, and 0.4 and 0.2 along the shortest axis. The object is seen after a rotation of 45 deg around the shortest axis, and 45 deg around the intermediate axis. The resulting shape is shown as a polyhedron, whose facets extend over 10 deg in longitude, and 5 deg in latitude.Credits: Cellino A. Hestroffer D., Lu X.-P., Muinonen K., Tanga P.: Astronomy & Astrophysics 631, A67, 2019
